Classification de Signaux Audio avec du Machine Learning

Introduction

Le projet consiste à développer un système capable de classer des signaux audio, précisément des mots et des voix de différents speakers, à l’aide de réseaux de neurones. L’objectif est d’atteindre une précision de classification élevée pour deux catégories : les mots prononcés (chiffres de 0 à 9) et le speaker (6 différents speakers)

Explication des programmes déjà fournis

1. Initialisation et Configuration

La phase initiale du projet consiste à établir un environnement de travail pour le traitement et la classification de signaux audio. Cette étape comprend la configuration de l’environnement de programmation et la gestion des dépendances.  Elle permet la mise en place du stockage et des librairies utiles.

Il nous a suffit de rajouter le chemin d’accès de notre google drive. 

La bibliothèque librosa est utilisée pour l’analyse audio, tandis que TensorFlow avec l’API keras servent à construire et entraîner les modèles de réseaux de neurones.

Le projet utilise le free-spoken-digit-dataset, qui contient 3000 enregistrements audio de chiffres prononcés en anglais par six orateurs différents. Chaque chiffre est prononcé 50 fois par chaque orateur, ce qui offre une variété suffisante pour entraîner les modèles de reconnaissance vocale.

Les données audio sont clonées directement dans le drive à partir de son dépôt Git. Cette méthode assure que les données les plus récentes et complètes sont utilisées pour le projet.

2. Génération de Spectrogrammes Mel

La transformation des signaux audio en spectrogrammes Mel est une étape qui convertit les signaux audio en une forme visuelle qui représente l’évolution des fréquences au fil du temps.

Les spectrogrammes Mel sont des représentations bidimensionnelles de signaux audio, où l’axe des x représente le temps, l’axe des y représente les fréquences des bandes de Mel, et l’intensité des couleurs indique l’amplitude. Ces spectrogrammes imitent la perception auditive humaine plus fidèlement que les spectres de fréquences linéaires.

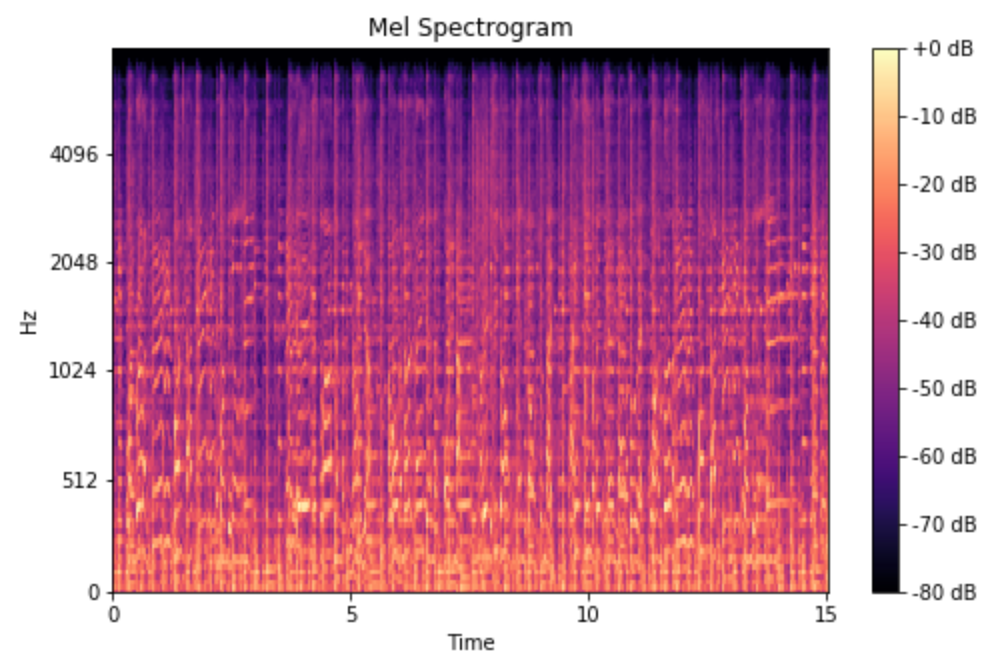
Pour chaque enregistrement audio, un spectrogramme Mel est calculé en utilisant la bibliothèque librosa. Ce processus implique plusieurs étapes :

• Chargement du fichier audio : Le signal audio est chargé en mémoire.
• Transformation de Fourier à court terme (STFT) : Le signal est segmenté et une transformation de Fourier est appliquée à chaque segment.
• Application de l’échelle Mel : Le spectre STFT est ensuite converti en échelle Mel, qui est une échelle de fréquences non linéaire plus cohérente avec la perception humaine du son.

Les spectrogrammes sont sauvegardés sur le drive pour être réutilisables. Le travail sur les spectrogrammes revient à travailler sur des images.

Première approche

1. Labélisation des données

Cette section du projet consiste à associer à chaque spectrogramme des labels pertinents pour le locuteur, le chiffre prononcé, et l’occurrence. Pour cela, les données ont comme convention “chiffre_speaker_occurence”, on extrait donc le label et on l’associe dans les listes correspondantes.

Les données sont converties en tableau numpy de dimensions (3000, 128, 36, 1), où 3000 représente le nombre total de spectrogrammes, 128 et 36 sont les dimensions des spectrogrammes, et 1 indique un seul canal de couleur (niveaux de gris). Cette organisation permet d’utiliser toute la théorie sur la manipulation d’image numpy.

2. Séparation en données de Train et de Test 

Pour la réalisation du dataset, il est nécessaire de séparer les données en deux sous-ensembles distincts : l’ensemble d’entraînement (Train) et l’ensemble de test (Test). Cette séparation est cruciale pour évaluer de manière fiable la performance du modèle de reconnaissance de la parole que nous développons, en assurant que le modèle est testé sur des données qu’il n’a jamais “vues” durant l’entraînement. La répartition donne 20% de données de tests et 80% pour l’entraînement.

Cette répartition a été effectuée de manière aléatoire pour chaque combinaison de locuteur et de chiffre, en utilisant une permutation aléatoire des indices de chaque classe, garantissant ainsi que les données d’entraînement et de test sont variées et représentatives. En effet, on souhaite éviter un “overfitting” sur les données d’entraînement et obtenir des performances homogènes dans les deux ensembles.

La distribution des classes dans les ensembles de données formés a été vérifiée pour s’assurer de leur homogénéité, utilisant la fonction OccurencesClasses. Les résultats montrent une répartition équilibrée :

• Ensemble d’entraînement : 2100 instances, avec chaque chiffre présent 210 fois et chaque locuteur présent 350 fois.
• Ensemble de test : 900 instances, avec chaque chiffre présent 90 fois et chaque locuteur présent 150 fois.

On obtient bien les 3000 enregistrements répartis de manière homogène dans les deux ensembles dans les bonnes proportions.

3. Mise au format pour le réseau

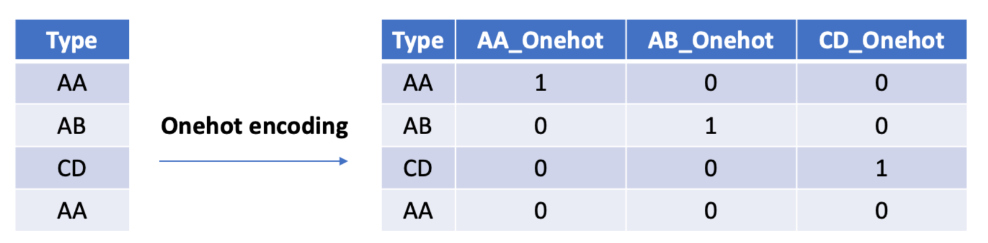
La préparation des données pour l’entraînement d’un réseau de neurones implique de transformer les ensembles d’entraînement et de test en formats compatibles avec les exigences de l’architecture réseau utilisée, notamment les couches de convolution qui requièrent des entrées sous forme de tenseurs et tableaux numpy. Pour cela, nous utilisons la fonction “to_categorical” qui transforme les étiquettes numériques en vecteurs binaires sous forme de one-hot encoding, permettant au réseau de prédire la probabilité pour chaque classe indépendamment.

Data Science in 5 Minutes: What is One Hot Encoding?

En effet, à chaque classe est associée un vecteur ayant un seul ‘1’ qui indique la classe de l’observation (par exemple pour le chiffre 1 le vecteur sera : (1 0 0 0 0 0 0 0 0 0)), les autres valeurs étant des ‘0’. En pratique, le réseau prévoit des probabilités pour chaque classe et essaie de faire correspondre ces probabilités au vecteur one-hot de l’étiquette.

On obtient la dimensions des étiquettes encodées (train par exemple), (2100,10), indiquant que chaque étiquette de chiffre a été transformée en un vecteur de 10 classes.

4. Conception du réseau (architecture)

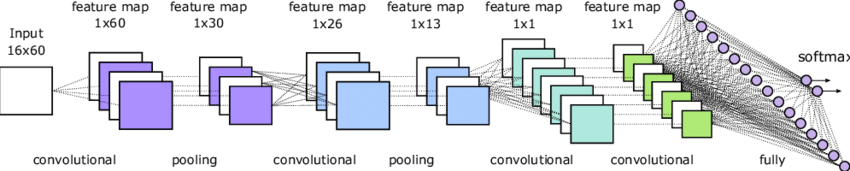
Full architecture of the CNN. Each box is a feature map in different… | Download Scientific Diagram 

Pour cette partie, nous avons conçu un réseau de neurones convolutifs (CNN) dans le but de reconnaître les chiffres prononcés à partir des spectrogrammes Mel. Ce qui revient à faire de la reconnaissance d’image. 

Dans une couche convolutive, chaque filtre est comme une caméra ajustée pour reconnaître un motif dans l’image. Par exemple pour le premier filtre, on a 64 filtres, de dimension 10×10 pixels. Chaque filtre glisse sur l’image pixel par pixel, de haut en bas et de gauche à droite. Le neurone est activé si le filtre reconnaît la zone comme des bords, des formes spécifiques. Une fois toutes les images parcourues, on obtient une nouvelle collection de 64 images (une pour chaque filtre), chacune montrant différentes caractéristiques capturées de l’original. (La taille de chaque image est réduite à 119×27, car le filtre ne peut pas glisser au-delà des bords de l’image originale de 128×36 sans sortir de celle-ci).

La couche Max Pooling 2D agit comme un processus de réduction, où l’on résume les informations les plus importantes des images obtenues de la couche précédente. On peut visualiser cela comme un petit cadre de 2×2 pixels (exemple) qui glisse sur chacune des images. À chaque étape, ce cadre ne garde que le pixel le plus lumineux (ou le plus important) parmi les quatre qu’il couvre, et ignore les autres. En ne conservant que le pixel le plus important de chaque groupe de quatre, cette opération réduit de moitié la hauteur et la largeur des images. Ainsi, une image qui était de taille 119×27 devient 59×13. Cela rend le réseau plus rapide et moins coûteux en calculs pour les étapes suivantes, car il y a moins de données à traiter. Le but de cette opération est de rendre le réseau plus robuste à de petites variations dans les images d’entrée. Ainsi, MaxPooling2D simplifie les images en réduisant leur taille tout en conservant les caractéristiques les plus pertinentes ce qui réduit les calculs nécessaires. 

Jusqu’à ce point, les données traitées par le modèle sont en trois dimensions (hauteur, largeur, profondeur). La couche Flatten prend ce tenseur 3D et “l’aplatit” en un long vecteur 1D pour un réseau de neurone dense, chaque pixel de la convolution est en entrée d’un neurone. C’est souvent sur cette couche que le nombre de paramètres est assez importants.

Une couche Dense interconnecte les sorties des neurones précédents dans chaque neurones dans un nouveau neurone qui s’active en fonction des poids. 

La dernière couche du réseau contient le même nombre de neurones que de classes. Leurs sorties indiquent la probabilité de la classe correspondante. Avec le vecteur de sortie, on peut en déduire la classe probable de l’image d’entrée. 

Dans notre étude  :

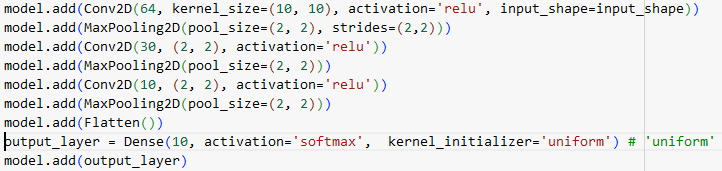
La taille des paramètres se calcule de la manière suivante : (Taille du filtre x Nombre de canaux d’entrée + 1 (biais)) x Nombre de filtres. 

Par exemple 1210 s’obtient par le calcul suivant : (2*2*30+1)*10.

5. Entraînement

Pour cette étape, on sélectionne les étiquettes encodées pour l’entraînement puis on entraîne le modèle en choisissant le nombre d’époque, la taille des lots et les données de tests.  Un lot est un ensemble d’échantillons de l’ensemble de données, sa taille détermine le nombre d’échantillons à traiter avant de mettre à jour les poids du modèle. Chaque itération correspond au nombre de lots nécessaires pour compléter une époque. Une époque correspond à un cycle complet de parcours à travers les données de test.

Par exemple, pour 1 000 échantillons et une taille de lot de 500, il faudra 2 itérations pour compléter une époque.

6. Prédictions et matrice de confusion

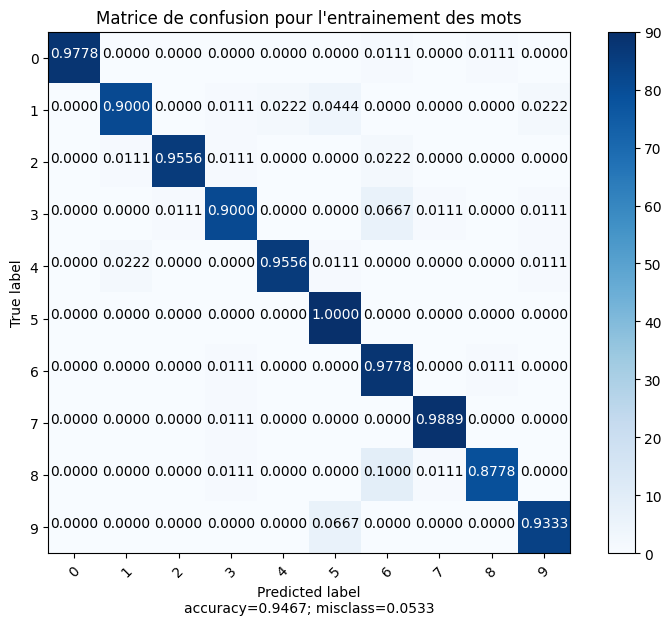
A partir du jeu de poids obtenu avec les données d’entraînements, on obtient un modèle qui permet de déterminer la classe d’une image. Puis, on compare les résultats obtenus avec ceux réels afin d’obtenir la matrice de confusion. 

L’axe “True label” représente les classes réelles et l’axe “Predicted label” représente la classe prédite par le modèle. Chaque case [i,j] indique le pourcentage de labels de la classe i (classe réelle) qui ont été classés comme la classe j (classe prédite). Sur la diagonale, on retrouve le pourcentage de données correctement prédites pour la classe qui se trouve en abscisse et ordonnée. Par exemple, pour la classe “0”; 97,78 % des données de tests ont été correctement prédites. En revanche, 1,11 % des 0 ont été interprétés comme de – et 1,11% comme des 8.

On obtient une accuracy de 94,67 % ce qui signifie que 94,67 % des données de test ont été correctement classées par le modèle. En revanche, 5, 33 % des données de test ont été mal classées par le modèle.

7. Réseau classification du speaker

On reprend la démarche précédente pour le choix du modèle, l’entraînement avec les données d’entraînement des “speakers”, sauvegardé le jeu de poids obtenu avec les données d’entraînement, on obtient de la même manière la matrice de confusion. Le réseau réussit à prédire correctement le speakers à 96,33 %. La démarche est identique.

Conclusion de la partie : Nous avons entraîné deux réseaux de neurones, un pour reconnaître les mots, l’autre les speakers. Tous deux donnent des prédictions avec une probabilité supérieure à 90%.

III. Prédiction par méthode ensembliste

L’approche statistique consiste à combiner les prédictions de plusieurs modèles pour obtenir une meilleure performance que si on avait utilisé qu’un seul modèle. 

Il s’agira dans un premier temps d’entraîner trois modèles qui diffèrent tout d’abord par leur structure. Chaque modèle servira à faire des prédictions que l’on agrège par la suite afin d’obtenir une prédiction finale. Dans notre cas, la classe prédite le plus de fois sera dans l’idéal sélectionnée par tous les modèles. 

On demande en cas d’arbitrage, une information sur le niveau de confiance du résultat. On implémente alors un coefficient de confiance k, il varie de -1 à 1 donnant l’information : “certitude confiante” pour k = 1, “avec réserve” pour k = 0 et “indécision” pour k = -1. En cas d’indécision, le programme retourne la classe ayant la plus grande probabilité d’être choisie par un des modèles. 

Le début du projet débute de la même manière que précédemment : importation des bibliothèques/des données; connexion au google drive puis labellisation et séparation du dataset en données test et train.

1. Mise en place des réseaux et prédiction

 1.1 Environnement de travail

Pour plus de flexibilité dans les fonctionnalités, nous avons développé un objet “Model1” héritant de l’objet Sequential de Keras. Cela nous permet d’encapsuler les fonctionnalités spécifiques au modèle de cette partie.  Le préfixe permet d’initialiser différents jeux de poids en fonction du contexte. Et l’id de structure permet de choisir une structure parmi toutes celles prédéfinies dans le code. L’objet embarque des fonctionnalité pour la sauvegarde, le chargement de poids, l’entraînement et la création de l’architecture. 

Pour les mêmes raisons, l’objet “DétecteurMots” regroupe l’ensemble des fonctions pour faire une prédiction. Ainsi, il contient une liste de p modèles, ayant les caractéristiques et la structure donnée par le constructeur. L’objet a des fonctionnalités pour : entraîner tous les réseaux de sa liste, les entraîner, les sauvegarder, les charger, et prédire par agrégation une classe en estimant un niveau de confiance. 

1.2 Agrégation

Pour réaliser une prédiction avec 3 modèles de structures de réseau, on utilise les instructions suivantes : 

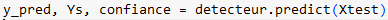
L’objet détecteur retourne la classe prédite par agrégation, les classes prédites par chaque modèle. On présente ici le corps de la fonction de prédiction : 

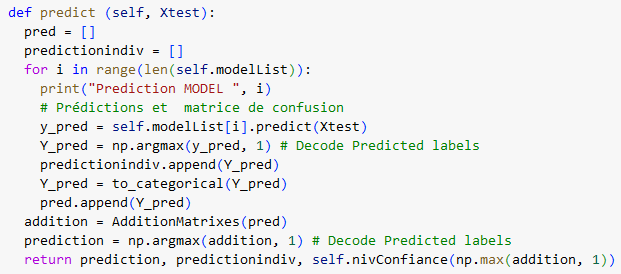
Cette prédiction utilise un vecteur “addition” et la fonction addition pour déterminer sous la forme de Onehot les occurrences de classes (La fonction est similaire à occurrence classe mais permet de travailler sur une liste). De plus une fonction annexe nivConfiance permet d’estimer la confiance en comparant les probabilité d’obtention de la classe.

On peut donc tracer les  matrices de confusions, d’abord des 3 modèles indépendants puis de l’agrégation. 

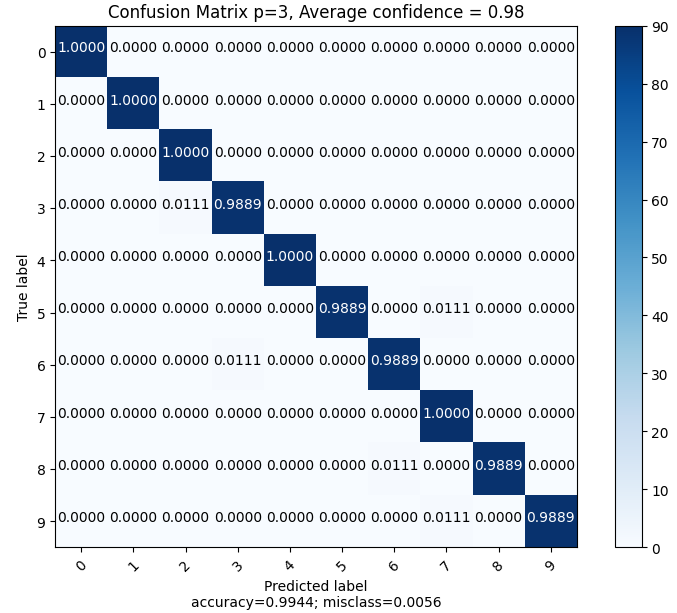
On peut donc lire une précision de 99.33%, 99%, 98.67% pour les modèles individuels et un résultat avec une précision de 99.44% avec une confiance moyenne de 0.98 (très proche de “avec confiance” à chaque agrégation). Ainsi, la moyenne statistique sur trois réseaux différents permet de “compenser” les biais de l’un ou l’autre modèle assurant une précision supérieure en combinant les résultats que pris individuellement.

2. Pour aller plus loin : Plus de réseaux !

Le modèle précédent fonctionne déjà bien, on peut essayer d’aller plus loin en ajoutant plus de modèles à notre étude. Pour comparer, on va aussi utiliser la même architecture. Cette idée n’est pas la meilleure, en effet garder la même architecture va réduire cet effet de “compensation” que nous avions précédemment. On ne peut compter que sur la différence des poids issus de l’entraînement pour faire la compensation en cas d’erreur.

Le code de la dernière partie est réutilisable car assez versatile pour cette application. De plus, pour accélérer l’entraînement, on a rajouté une condition d’arrêt, si la précision dépasse 90%, on considère le modèle entraîné et on passe au suivant. Les couches dropout prennent tout leur sens car lors de cet entraînement, on constate que certains réseaux peines à converger. Ajouter un peu d’aléatoire aide donc à sortir de l’impasse.

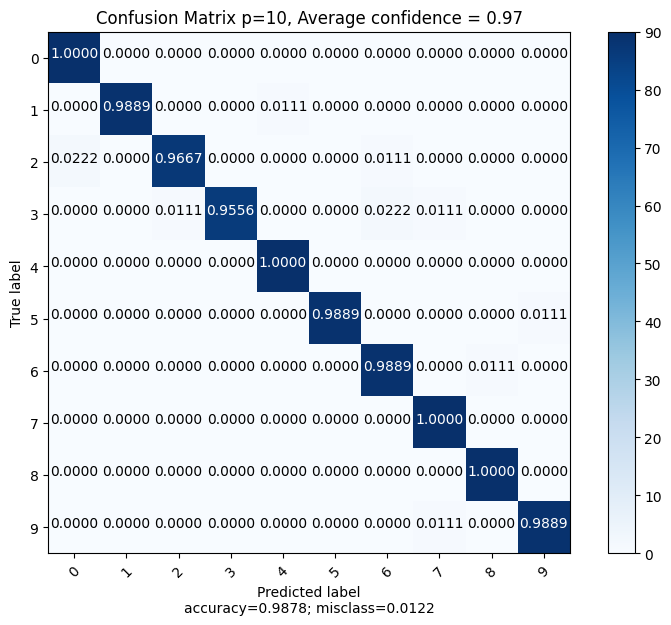
On obtient une précision globale de 98.78%, ce qui  est moins bien que dans la dernière étude comme prévu. Par ailleurs, limiter l’entraînement des réseaux a aussi un impact direct sur la précision obtenue. On note pour les précisions individuelles, une majorité des réseaux avec une précision de 96%. Donc globalement on améliore toujours la précision par rapport à un unique réseau. 

3. Pour aller toujours plus loin : Transformée de fourier.

Dans les dernières parties, nous avons l’impact de deux paramètres : modifier la structure du réseau, et le nombre de réseau. Nous allons maintenant changer le type de donnée d’entrée. Pour cela nous allons reprendre toute l’étude et la faire sur la FFT au lieu de travailler avec les MEL-spectrogramme. Il faut donc adapter l’entièreté des étapes du projets : convertir les données audio en donnée spectrale type FFT, les enregistrer sur le drive, les labelliser, les séparer en deux parties (train et test) et enfin appliquer les modèles. 

Pour rappel la FFT est une méthode du calcul de la transformée de fourier discrète, elle décompose un signal en ses composantes fréquentielles qui sont alors utilent pour la détection de motifs périodiques.

Les objets Model1 et Détecteur Mot sont pensés pour travailler avec tout type d’images, les modifications ne vont donc pas les concerner et on pourra les utiliser tel quel en renseignant les bons paramètres associés à la transformée de Fourier. 

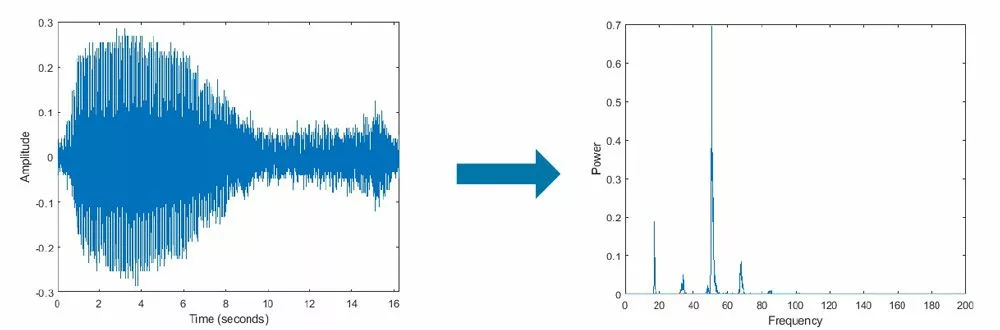
https://fr.mathworks.com/discovery/fft.html

On se propose d’entraîner 5 modèles différents sur les données issues de la FFT. 

Les résultats sont légèrement moins bons car, les images étant plus grandes, l’entraînement a été raccourci et les modèles de bases sont moins précis. (environ 91%).  On obtient tout de même une précision acceptable de 95.44% avec une certitude de 0.92 donc assez confiant. 

On peut maintenant faire l’agrégation avec l’autre méthode, ainsi les deux types de données pourront se compenser.

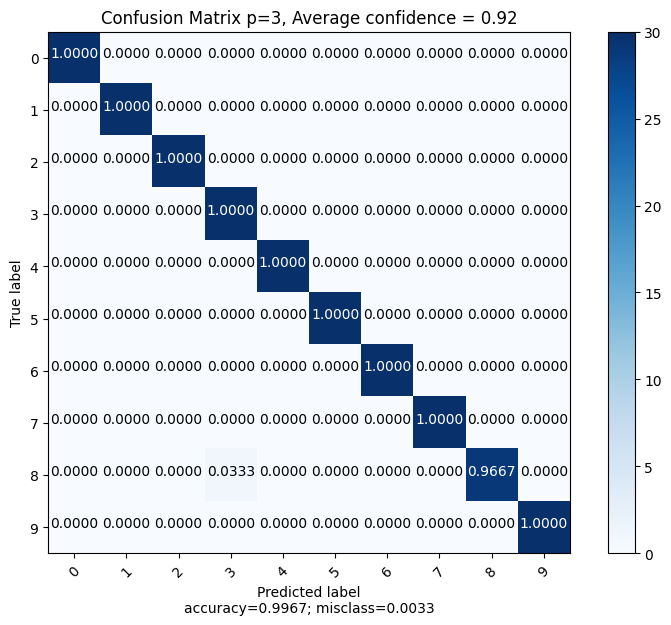
On observe alors qu’en combinant les deux méthodes, on obtient une précision de  99.67% ce qui est bien supérieur à ce que l’on trouvait avec toutes les méthodes précédentes. 

Il est donc intéressant de varier à la fois, les types de données d’entrées, mais aussi les structures des modèles utilisés ainsi que le nombre de modèles. Plus il y a de modèle, plus on a de probabilité de trouver la bonne classe.

Cependant, on a pu remarquer au fil du projet que générer autant de modèles différents a un coût. Un coût à la fois de calcul, le temps requis pour entraîner et activer les neurones augmente avec le nombre et la complexité des modèles. Ainsi qu’un coût de stockage non négligeable. Environ 1Gb pour les jeux de poids de la FFT et 150Mb pour le MEL par exemple. 

Une partie intéressante à creuser serait de chercher à optimiser le réseau de neurones pour obtenir des résultats satisfaisants sans avoir à utiliser autant de paramètres. Ici, on supposait avoir un espace de stockage suffisant et une force de calcul raisonnable.  Mais on se rend compte que les modèles utilisés, bien que très performants, sont trop volumineux par rapport à la tâche demandée.