Modélisation d’un panneau photovoltaïque – Dimensionnement
Ce projet a été réalisé en collaboration avec Thémi’s et les professeurs du L2EP.
Introduction
Au vu des enjeux énergétiques récents, il est intéressant de développer des sources d’éner-
gies non polluantes à l’échelle humaine. L’énergie solaire en fait partie. De façon directe ou
indirecte, il est possible de récupérer une partie de cette énergie et de la convertir en électricité.
Notre étude se limitera à l’énergie rayonnée par le soleil captée par un panneau photovoltaïque.
(≈ 175.109 MW reçus par l’atmosphère en permanence [1]).
L’énergie émise par le soleil n’est pas parfaitement convertie. L’atmosphère, les conditions
climatiques, la commande du panneau et la localisation géographique modifient le rendement.
Il est donc primordial de comprendre l’influence de ces paramètres pour optimiser l’énergie
convertie. Il existe différentes technologies, indirectes (biomasse, hydraulique, éolien…) et di-
rectes (thermique, thermodynamique, photovoltaïque) [2]. Dans l’ensemble de l’étude, on
considèrera un panneau photovoltaïque positionné dans le Nord de la France (Lille), orienté
à 30°, plein sud. Cette orientation permet d’obtenir un rendement maximal. [2].
Un panneau photovoltaïque est composé de cellules photovoltaïques, elles-mêmes composées
de deux électrodes et de plusieurs couches de semi-conducteurs. Un apport énergétique d’éner-
gie crée une différence de potentiel et donc un courant si le circuit est fermé.
Plusieurs technologies de semi-conducteurs existent, les plus utilisées étant le silicium mono-
cristallin, dont le rendement moyen est assez élevé (12,8%) mais son coût est élevé. On retrouve
aussi le silicium polycristallin, moins coûteux mais également moins efficace. Le rendement
moyen étant alors de 12,6%. L’usage de silicium amorphe est aussi possible. Bien que cette
technologie soit la moins onéreuse, le rendement de celle-ci est faible puisqu’il est d’au mieux
8%. D’autres technologies existent, notamment le tellurure de cadmium, et les alliages de cuivre
indium/gallium sélénium. [2]
Le choix de la technologie précise est éludé pour simplifier l’étude. On considèrera le panneau
comme un modèle type “boite noire”. Plusieurs fois dans l’étude, nous approximerons le panneau
solaire à une source de courant idéale par un souci de simplicité. Toute l’étude sera simulée sur le
logiciel Matlab Simulink en utilisant les composants Simscape spécifiques à l’électrotechnique.
Objectifs
Étudier le panneau voltaïque fourni, mettre en place une commande pour extraire le maxi-
mum de puissance et raccorder le système au réseau.
1/ Etude du panneau photovoltaïque
Pour comprendre la réaction du panneau, nous avons commencé par étudier la caractéris-
tique courant/tension et la puissance fournie par le panneau en fonction de certains paramètres.
1.1 Variation de l’éclairement
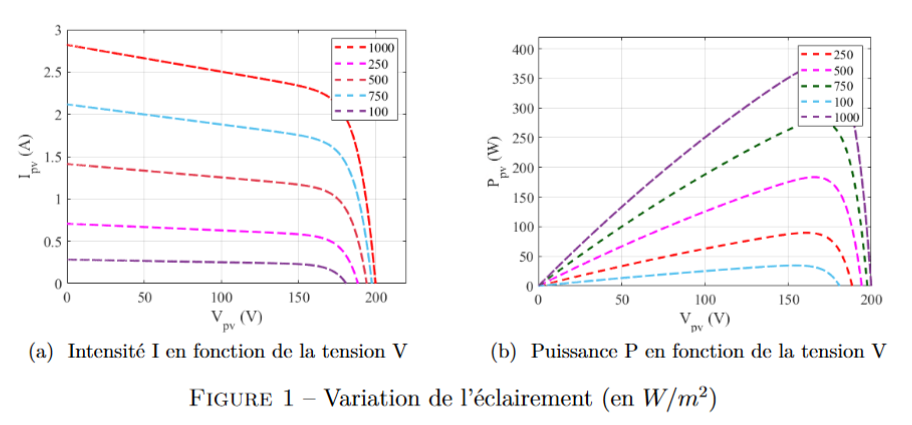
La caractéristique courant/tension est donnée figure 1(a). Elle permet de prévoir à une
tension imposée, le courant qui sera fourni par le panneau. On observe sur la figure 1(b) qu’il
existe un point particulier à chaque caractéristique, il se nomme le MPP (Maximum Power
Point) et correspond au point de puissance maximale, le couple courant/tension alors déter-
miné correspond au point de fonctionnement optimal. On observe que le MMP augmente avec
l’éclairement. Physiquement on comprend bien que il y d’énergie disponible sur le panneau
solaire, plus celui-ci la convertie.
1.2 Variation de la température
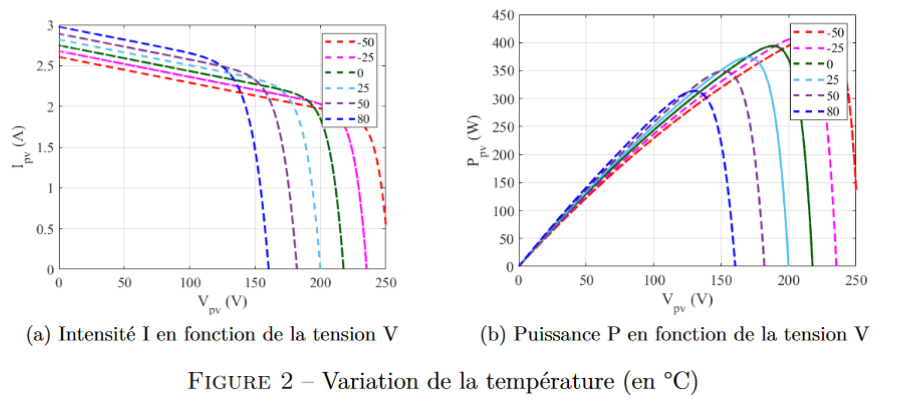
On observe donc sur la figure 2(a) les différentes caractéristiques en fonction de la tempé-
rature, on remarque que la tension maximale admissible pour obtenir un courant augmente de
façon significative avec des températures faibles. Sur la figure 2(b) on observe une diminution
du MPP quand la température diminue.
Le panneau solaire fonctionne donc mieux avec un ensoleillement maximal et une faible tem-
pérature. Il faut donc adapter la commande en fonction de ces paramètres pour extraire un
maximum de puissance.
2/ Conversion
2.1 Hacheur DC/DC
Notre panneau photovoltaïque doit, dans un premier temps, être capable de recharger une
simple batterie même si cette dernière n’a pas la même différence de potentielle. Pour cela
on réalise un montage hacheur, composé d’un . Selon les règles de l’électrotechnique, il faut
respecter l’alternance des sources. Le panneau photovoltaïque se comporte comme une source
de courant et la batterie comme une source de tension. On pourrait donc théoriquement les
relier directement au hacheur comme sur la figure 3a.
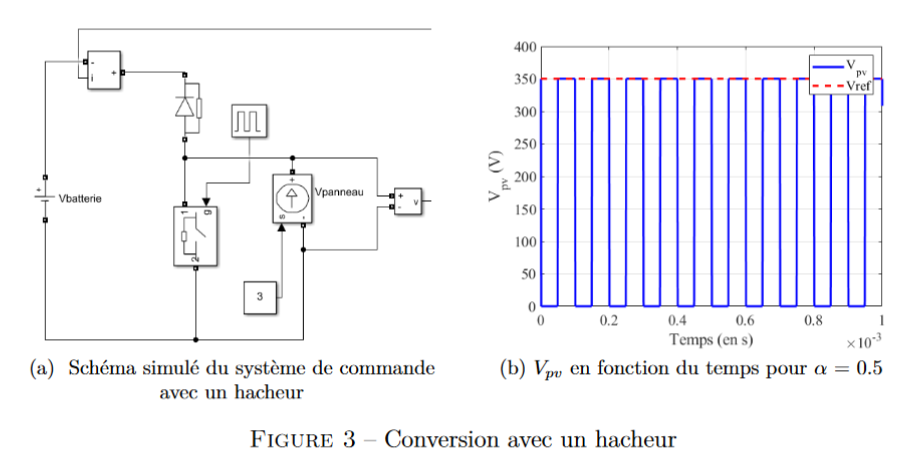
On peut donc commander le panneau en modifiant le rapport cyclique du hacheur. La
commande est un signal créneau à l’état haut pendant αT à chaque période. La valeur efficace
de la tension au borne du panneau est alors αE.
Pour une tension Vdc donnée de batterie et Vref consigne du panneau, on trouve :
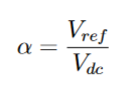
Cependant on remarque lorsque que l’on simule la recharge de la batterie 3b, il y a des
variations brutales de tensions et donc de courants (avec la caractéristique donnée figure 1)
qui peuvent endommager le panneau solaire, il faut donc trouver un montage qui lisse cette
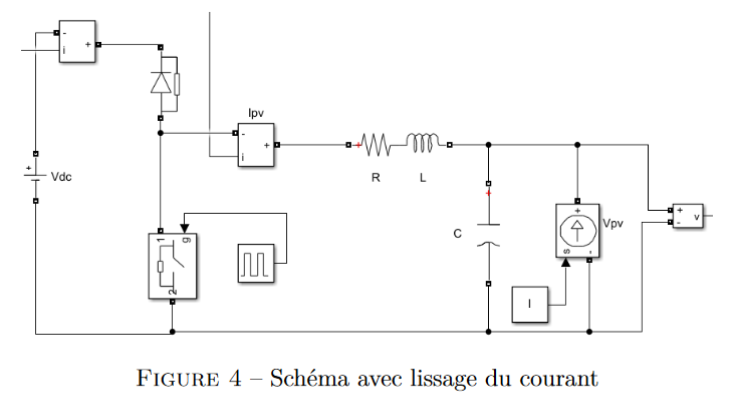
grandeur au cours du temps. On ajoute donc une inductance en série avec le panneau et un
condensateur en parallèle (pour respecter l’alternance des sources). Le schéma devient alors la
figure 4 et alpha se calcul en prenant en compte la chute de tension due à la résistance de la
l’inductance. La loi des mailles donne donc :
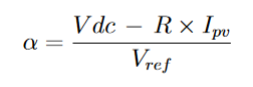
2.2 Dimensionnement de L et C
Pour dimensionner les composants, on nous impose des variations de tensions et de courants
notées ∆Vmax et ∆Imax à 1% de la valeur nominale de V et 5% de I. On cherche donc à exprimer
ces variations dans le circuit. On a Vdc cosntant et Vpv périodique donc :
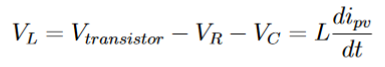
On peut négliger la chute de tension induite par la résistance.
Entre t=0 et t=αT :
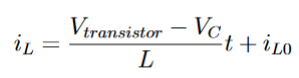
De la même façon entre t = 0 et t = αT :
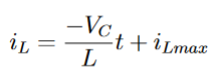
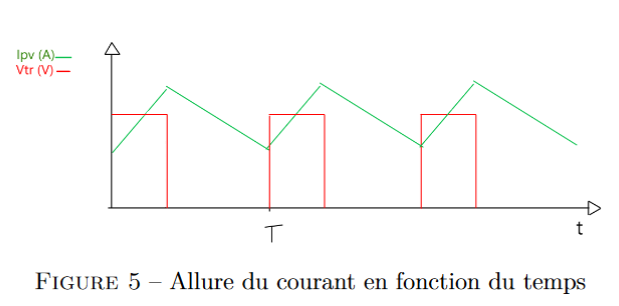
Sur la figure 5, on a donné l’allure de l’ondulation du courant. On peut donc exprimer la
continuité en αT qui donne :
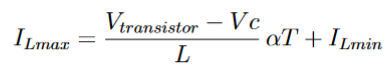
En exprimant la variation dans le circuit, on obtient :
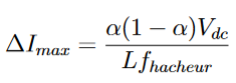
On fait la même chose pour la variation de tension et on obtient :
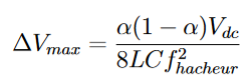
On peut alors en déduire les valeurs de L et de C, qui donnent : L = 583 mH et C = 1,071 μF.
3/ Asservissement
Un asservissement permettra de contrôler précisément le point de fonctionnement du pan-
neau solaire. On cherche ici à asservir deux grandeurs.
3.1 Asservissement du courant
Pour l’asservissement en courant, on met en place un asservissement par hystérésis. Le
principe est simple, on impose une variation de courant, une consigne et créé alors un espace
borné entre deux valeurs extremums. On va donc contrôler le transistor en fonction de l’état
du courant. Pour cela on utilise la logique combinatoire et une porte mémoire RS (SR Latch)
dont le fonctionnement est donnée figure 8. On peut donc augmenter et baisser le courant en
fonction de la situation.
On compare donc le courant actuelle avec la consigne + ∆Imax/2 et la consigne – ∆Imax/2.
Et en fonction, on augmente ou diminue le courant. Cet asservissement permet de toujours
osciller autour de la consigne et de respecter le cahier des charges imposé.
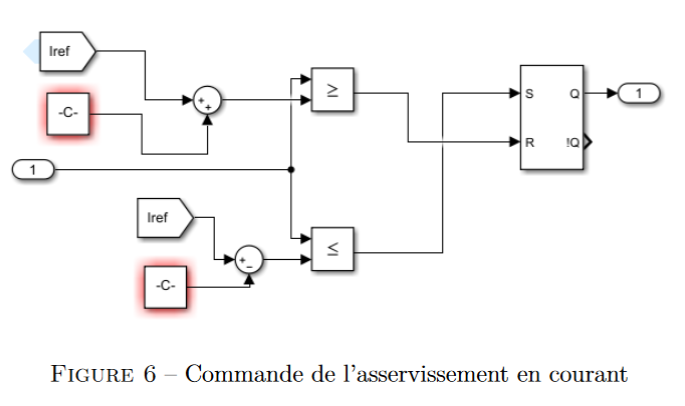
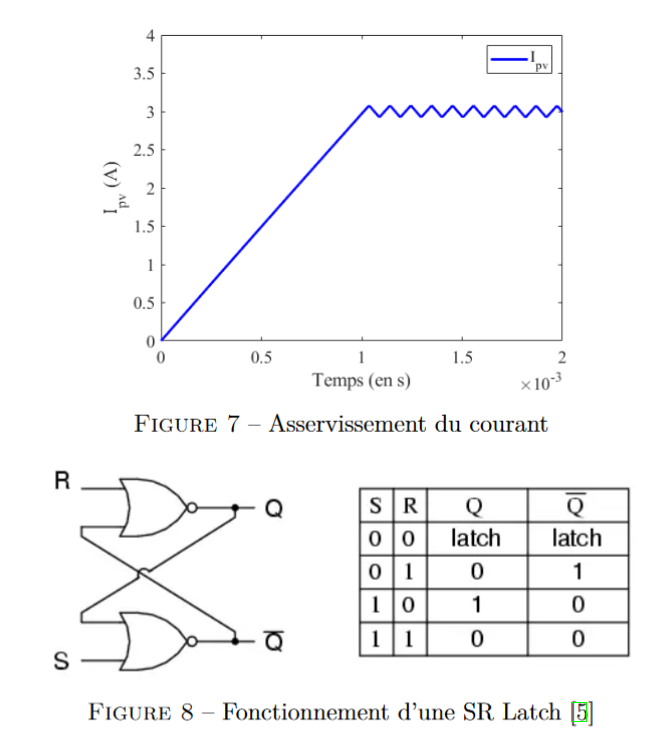
Nous l’avons donc implémenté dans matlab sur la figure 6. Et nous obtenons la courbe
présenté 7. On observe donc bien que le courant croît jusqu’à entrer dans la zone bornée, de là,
il ne peux plus s’en échapper
3.2 Asservissement de la tension
Pour réaliser cet asservissement en tension, nous avons du implémenter un correcteur à
notre circuit. Plusieurs choix se présentaient à nous :
- le correcteur proportionnel, mais bien que parmi les solutions possibles il soit le plus
simple à paramétrer, il ne corrige pas l’erreur statique - le correcteur proportionnel intégral (PI), qui corrige l’erreur statique, mais pas l’erreur
dynamique - le correcteur proportionnel Intégral et Dérivatif (PID), qui corrige les erreurs statiques et
dynamiques mais est difficile à dimensionner
Pour simuler l’action du condensateur dans la boucle de commande, nous avons utilisé un
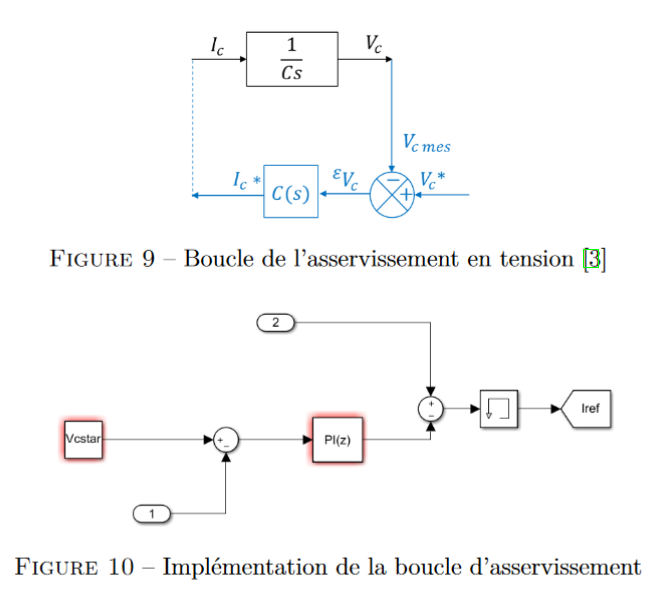
intégrateur de gain 1/C . De plus, on cherche donc à réaliser une boucle d’asservissement. Elle peut
se mettre sous la forme suivante : figure 9 (proposé par le L2EP [3]). On agit sur la consigne
en courant pour imposer la tension. L’implémentation sous matlab est présentée figure 10.
Nous avons opté pour un correcteur PI, plus simple à paramétrer que cette dernière solution.
La fonction de transfert d’un tel correcteur s’écrit kp + ki. Ce qui nous permet de déterminer
la FTBF (Fonction de transfert en boucle fermée) du circuit corrigé :
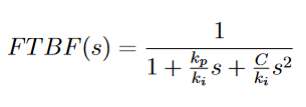
Aussi, la FTBF du circuit exprimée en fonction du coefficent d’amortissement ξ et de la
pulsation propre ωn est :
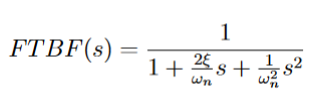
On peut alors identifier les paramètres du correcteur : ki = Cω^2n et kp = 2ξCωn.
Nous souhaitons obtenir la correction la plus rapide sans dépassement, nous choisissons donc
ξ = 1.
ous avons imposé un temps de réponse de 1ms (suffisant pour être assez rapide aux vues
des perturbations extérieurs et assez lent pour ne pas déstabiliser le système), puis par lecture
des abaques on a ωn = 4744 rad/s.
Pour évaluer l’efficacité du correcteur, nous avons introduit deux perturbations, en assimi-
lant le panneau photovoltaïque à une source de courant idéale. La première, à 0,04s, est une
modification de la valeur d’intensité délivrée par cette source, qui passe de 3A à -3A. Nous
pouvons observer l’évolution de la tension aux bornes de cette source sur la figure 11a.
Nous avions imposé la tension à conserver à 180V, on remarque que la tension aux bornes du
panneau photovoltaïque était bien égale à cette valeur avant la perturbation. Après, la correc-
tion s’est rapidement effectuée, et la tension a bien été de nouveau égale à la valeur voulue. Ce
rejet de perturbation démontre l’efficacité de la correction pour une perturbation en intensité.On remarque aussi que le dépassement dû à la correction n’excède pas 1V, il n’y a donc aucun
risque que le panneau se détériore du fait de ce dépassement.
La deuxième perturbation a lieu à 0,5s, c’est une modification de la valeur de tension à
atteindre, qui passe alors de 180V à 90V. Nous pouvons observer l’évolution de la tension aux
bornes du panneau sur la figure 11b.
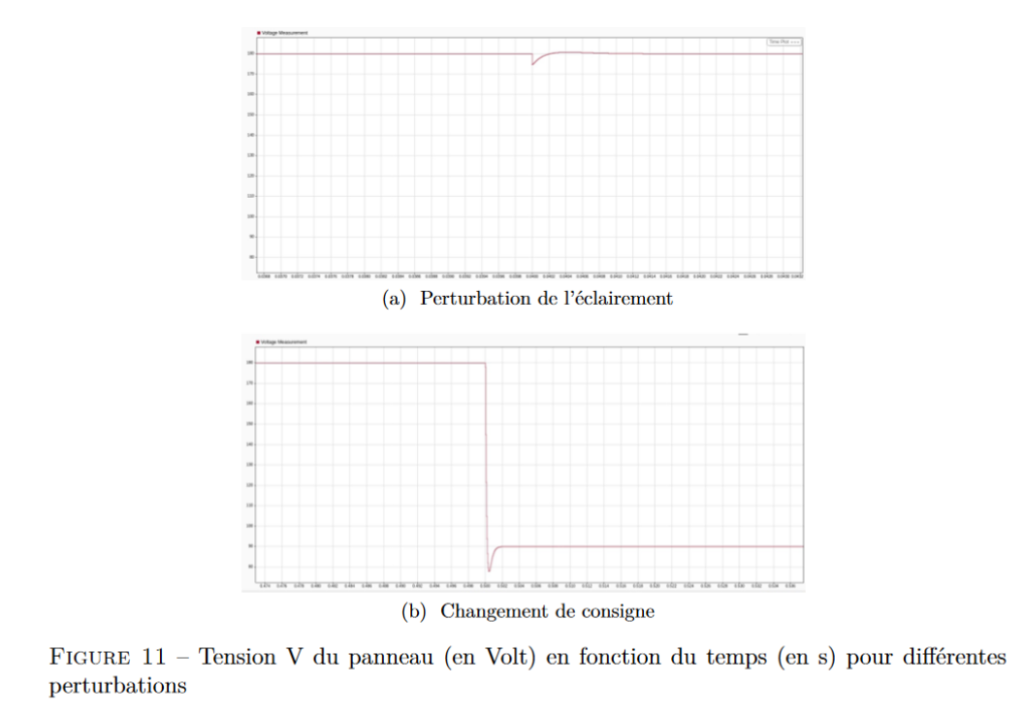
On observe que les valeurs désirées sont de nouveau atteintes : avant la perturbation, la
tension valait 180V, et après la correction elle atteignait bien 90V. Le correcteur permet donc
également de satisfaire à un changement de tension de consigne. La correction est toujours
brève, et il n’y a pas eu de dépassement.
La rapidité de correction, les rejets de perturbations et l’absence d’importance des dépasse-
ments, même lors de perturbation extrême (changement de signe de l’intensité) montrent que
notre correcteur a bien été dimensionné.
3.3 Recherche du MPPT
Comme nous pouvons l’observer grâce à la figure 1, pour une température et un éclairement
donnés, la puissance délivrée par le panneau photovoltaïque est maximale pour une valeur
spécifique de sa tension. Afin de maximiser le rendement, il est nécessaire qu’un asservissement
de Vref en fonction des paramètres extérieurs lui permette d’être égale à cette valeur optimale.
Nous avons donc mis en œuvre un algorithme MPPT (Maximum Power Point Tracking) à notre
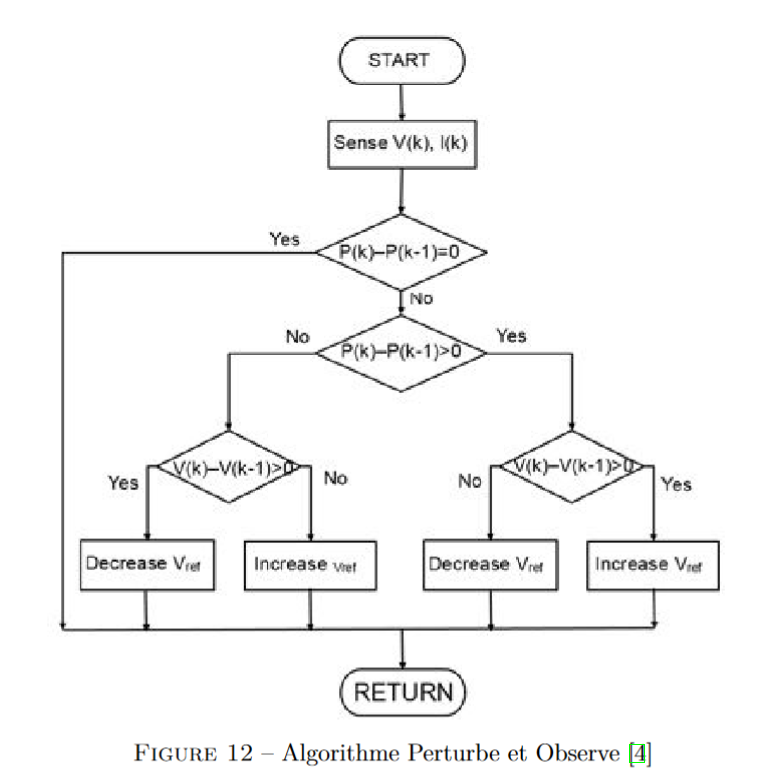
circuit, en utilisant la méthode Perturb and Observ (P&O). Le principe de cette méthode est
décrit sur la figure 12.
En analysant les valeurs de la puissance générée par le panneau photovoltaïque et de la
tension à ses bornes aux instant k et k-1, la tension Vref diminuera ou augmentera. Au final,
Vref égalera à tout instant la valeur permettant de générer une puissance maximale.
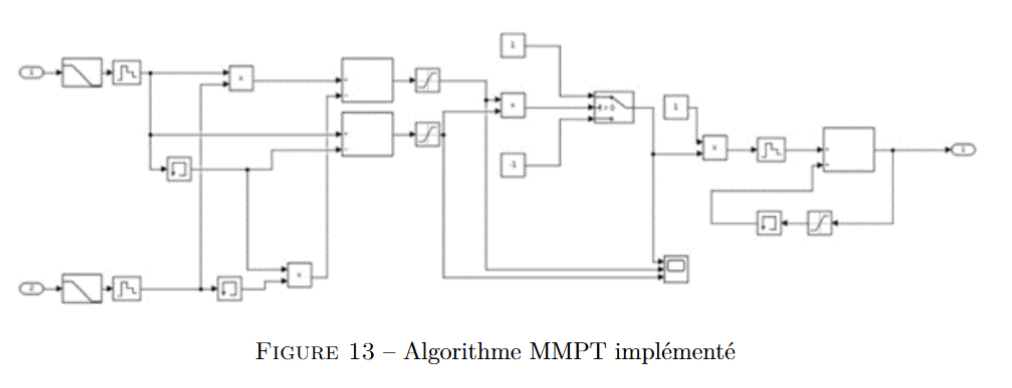
Sur Matlab, nous avons créé le circuit de MPPT présenté figure 13. Les entrées 1 et 2 étant
respectivement la tension aux bornes du panneau photovoltaïque et l’intensité le parcourant.
C’est une implémentation directe de l’algorithme avec quelques astuces propre à matlab, par
contrainte de temps, nous avons réutilisé celui proposé par le L2EP [3].
Notons qu’il est important de choisir un pas de calcul cohérent pour notre simulation, afin
d’assurer l’efficacité de la méthode. La valeur que nous avons retenue est 10−6s.
Après avoir intégré cet algorithme MPPT dans notre circuit avec panneau photovoltaïque,
nous avons vérifié son bon fonctionnement en modifiant les valeurs d’ensoleillement et de tem-
pérature pendant la simulation.
Avant les perturbations de température et d’ensoleillement, prévues respectivement à 0,333s
(figure 14) et 0,5s (figure 15), les puissances étaient constantes. Après chacune de ces perturbations,
nous avons observé un court état transitoire, durant lequel l’algorithme a asservi Vref à
la tension optimale, puis la puissance s’est stabilisée à une autre valeur, celle qui est maximale
dans les nouvelles conditions d’ensoleillement et de température.
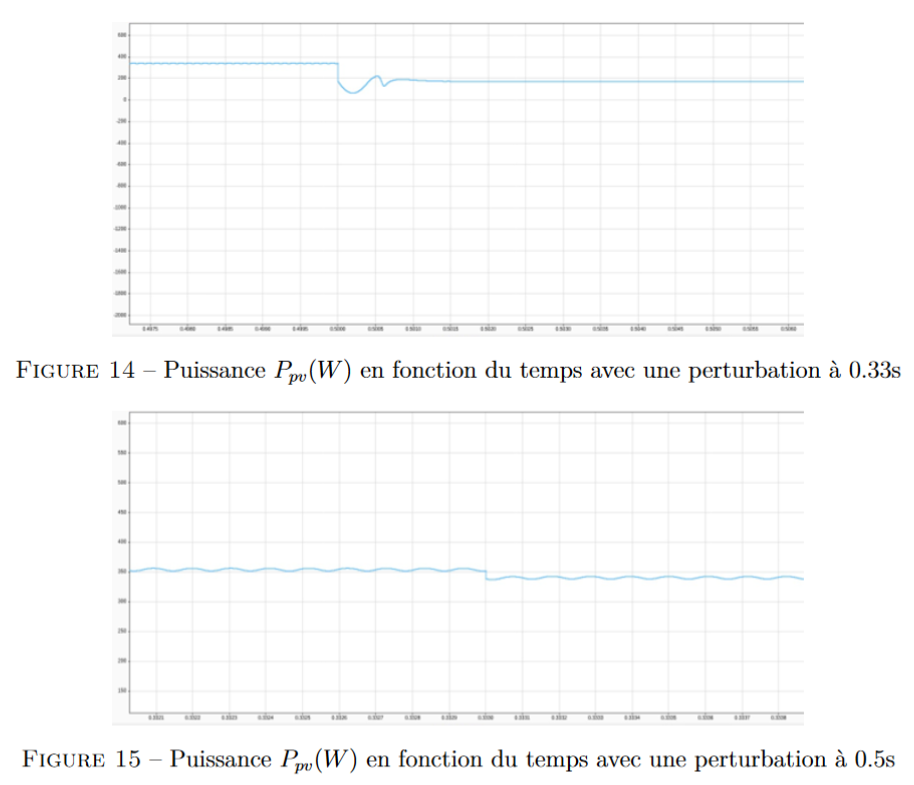
La rapidité de transition démontre également l’efficacité de l’algorithme puisqu’il illustre
bien le fait qu’à tout instant la puissance délivrée est quasi-maximale. En effet, en assimilant
ces perturbations à un passage nuageux, le temps de réponse du système est suffisant pour
perdre peu de puissance.
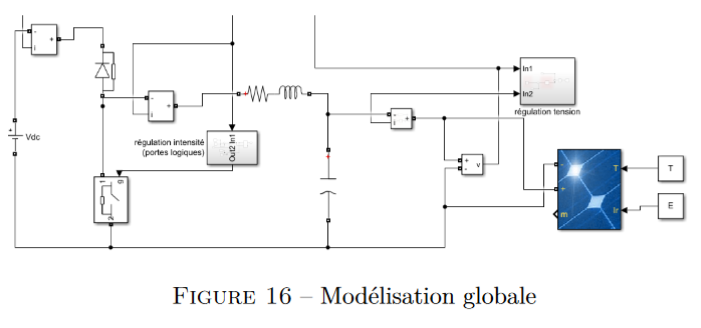
La simulation globale est présentée sur la figure 16. On peut retrouver les différentes par-
ties du systèmes qui fonctionnent ensemble pour placer le point de fonctionnement au MPPT
correspondant aux conditions extérieures actuelles.
4/ Raccordement au réseau
Nous n’avons pas pu aller jusqu’à cette étape pendant le projets.
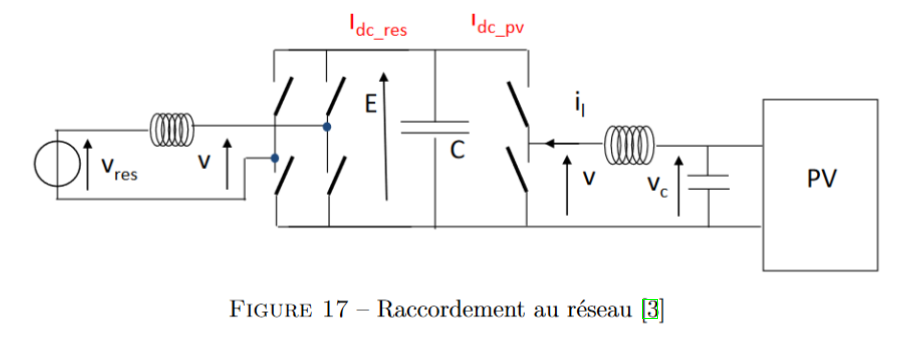
Le L2E P, propose un convertisseur DC/AC pour relier notre batterie au réseau et ainsi pou-
voir disposer de la puissance récupérée. Voici le montage correspondant (figure 17). Il fonctionne
à l’aide de deux cellules de commutations et d’une bobine qui assure l’alternance des sources. [3]
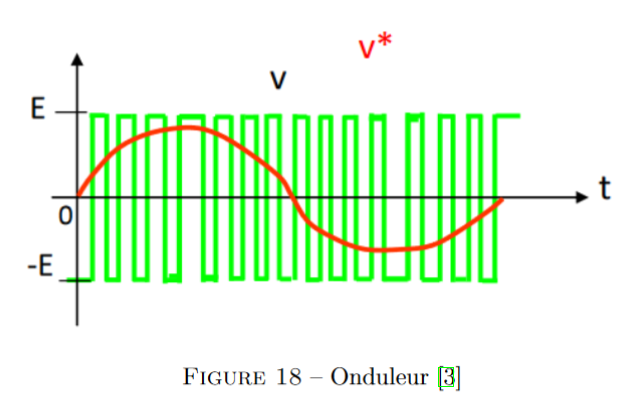
Pour onduler la tension de sortie, on fait onduler de façon sinusoïdale le rapport cyclique
régissant la commutation des cellules. On obtient alors une tension sinusoïdale comme présenté
sur la figure 18.
Conclusion
Nous avons réalisé une conversion DC/DC permettant de recharger une batterie, ainsi que
deux asservissements pour contrôler le point de fonctionnement du panneau photovoltaïque.
Nous avons ensuite réalisé un algorithme MPPT pour trouver le point de fonctionnement opti-
mal dans les conditions de fonctionnement avec la méthode Perturb and Observ. Nous n’avons
pas eu le temps de présenter un moyen de raccorder la batterie au réseau, nous avons cité la
solution proposé par le L2EP pour le faire.
Les objectifs fixés en début de projets sont partiellement atteints et la simulation informa-
tique ainsi créée peut être utilisée pour le contrôle de différents panneaux photovoltaïques car
les paramètres sont facilement modifiable dans le programme.
Références
[1] Dr. Bessemoulin P., Dr. Olieveri J. – Le rayonnement solaire et sa composante ultra-
violette, La Météorologie 8ème série, n°31, septembre 2000, cité p. 1
[2] Dr. Gruson François, Roillet Thomas, Dr. Delille Gauthier (EDF-R&D), “Intro-
duction au solaire photovoltaïque”, Arts & Métiers ParisTech CER Lille ; L2E P, 7 déc.
2016, cité p. 1
[3] Dr. Gruson François, Dr. Giraud-Audine Christophe, Projet 1A PV,Arts et Métiers
Science et Technologie Lille ; L2E P, 2019, cité p. 6, 7, 9, 11
[4] Crédit Image MPPT PO : “https ://fr.mathworks.com/solutions/electrification/mppt-
algorithm.html” – 1994-2024 The MathWorks, Inc p. 9
[5] Crédit Image RS Latch : https ://instrumentationtools.com/topic/s-r-latch/ – Inst Tools,
2024 p6